超高速開発に人工知能(AI)は寄与するか？

近年、これまでスクラッチ開発に重きを置いていた企業にも、超高速開発の気風が高まってきています。

超高速開発とは、システムの開発フローにおいて、設計・コーディング・テスト生成といった部分を自動化するための業務支援ツールを導入した開発手法を指します。

弊社では、キヤノンITソリューションズ製の「Web Performer」という超高速開発ツールを導入して、開発スピードを上げながら、より人間の智慧を必要とする部分にリソースを割く判断をしました。

このツールがどのような用途を持つかというと、例えばデータベースを設計するなら下記のような作業をスタッフが行います。

• データベース項目の登録
• 画面項目の登録
• 画面項目とデータベース項目の紐づけ

要はグラフィカルにデータベース設計が出来て、入力された要件に従い、指定された言語のコードが発行されるという仕組みになっています。

しかし、「システムを作るシステム」というと、SF好きでなくても、AIを活用した対話的なものを多少なり想像するのではないかと思います。 「要件定義→概要設計→詳細設計→実装→テスト→運用」という開発フローでいうなら、もっと要件定義部分に踏み込んでくるような製品を待ち望んでいるのは、きっと弊社だけではないでしょう。

そこで、もう少しAIらしい要素をもたせて、要件定義部分に踏み込むようなツールが作れないか、ということを考えてみました。

システム自動生成AIの機能案 - DB正規化をやってくれる

人間がデータベースを設計する時に、考慮せねばならないこととして、正規化があります。

データベース正規化というのは、ある程度経験のあるプログラマであれば、はじめから適切に正規化されたテーブルを作ることが可能です。開発のボトルネックになることはあまりないため、自動化できないかと真面目に考察したことのある方はあまり多くないのではないでしょうか。

しかし、データベースを含むシステムの生成をツール上で行う文脈であれば、ありもののテーブル（Excelワークシート、csvファイル、etc.）から勝手に正規化をやってくれたら、便利に感じるのではないかな、と着想しました。

本記事では、「システムを作るシステム」設計者の立場を仮定し、 正規化という概念を知らないようなユーザーでも、サンプルとなるテーブルを与えれば、正規化されたテーブルが出力されるようなアルゴリズムを考えてみたいと思います。

目的

第１正規形で与えられた任意の単一テーブルについて、ボイスコッド正規形への無損失分解を行うアルゴリズムを構築する。

ここで、用語の定義は下記の文献に則っていますので、適宜ご参照ください。

• 奥野 幹也，「理論から学ぶデータベース実践入門 ~リレーショナルモデルによる効率的なSQL」，技術評論社，2015．

第１正規形についての補足

入力が第１正規形であるということは、下記を満たすということを特記しておきます。

• 繰り返しグループ（同一セルに２つの値を含むなど）が存在しない
• データにNULLは含まれない

候補キーの検出

本記事で行うのは「候補キーの検出」までです。 得られた候補キー集合を用いてBCNFのテーブルを導くのは、今後の記事の内容となりますので、ご期待ください。

復習：候補キーとは？

候補キーとは、レコードを一意に特定できるようなカラムの集合のうち、既約(irreducible)なもの（の集合）を指します。

既約であるとは、候補キーから一つでもカラムを取り除くと、レコードを一意に特定出来なくなることを意味します。(irreducible = ir + reduce + ableですので、『減らせない』という意味ですね。)

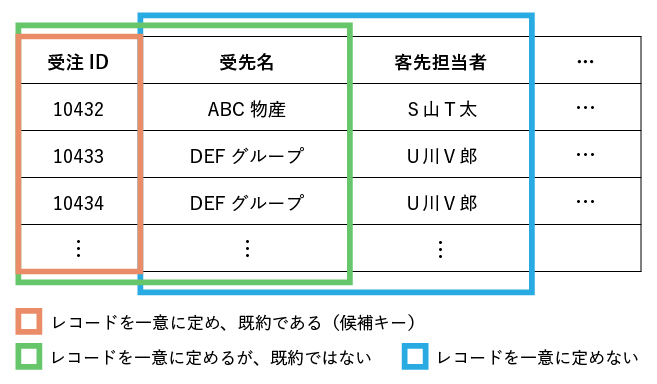
候補キーとなりうるカラム集合の数

まず、そもそもカラムの集合が何通りあるかを算定しましょう。 ここでは{受注ID，客先名，客先担当者，受注数，単価}という５つのカラムからなるテーブルを想定します。 ５つのカラムのうち、候補キーであるかどうか吟味すべきカラムの集合を、0/1の列で表すことにします。例えば(01101)は{客先名，客先担当者，単価}というカラムの組を指します。

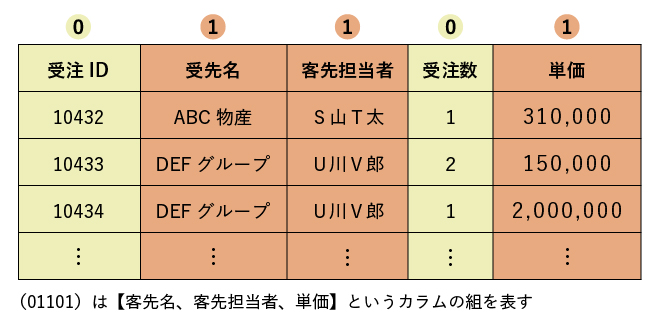
すべてのカラムからなる集合($11111$)は、もちろんレコードを一意に特定します。（そうでなければ、全く同じレコードがテーブル内に２つ以上存在することになりますが、それはリレーショナルモデルの仮定に反するため、ここでは考慮しません。）

さて、カラムの集合が何通りあるかですが、これは５桁の２進数のパターン数と等しくなることがお分かりでしょう。よって$2^5 = 32$通りのカラムの集合があります。一般に、カラム数を$n$とすると、$2^n$通りのカラムの集合があり、組合せ数はカラム数の指数オーダであることがわかります。 よって、すべての組が候補キーかどうかをナイーブに（愚直に）調べていると、確実に指数時間かかってしまいますので、効率化のための工夫をしたいところです。

二分木の導入

カラムの集合が候補キーであるか、どのような順番で検証していくかを決めるために、二分木(Binary tree)を導入します。 カラムが５つの例の場合、対応する二分木は第１〜第５階層まであり、各階層がカラムに対応します。そして、ノードの0/1値はその階層に対応するカラムを、候補キーであるか吟味すべき集合に含めるか含めないかを表しています。二分木の先端である葉ノード(leaf node)がカラムの集合を表します。例えば二分木の根(root)からある葉ノードまでの経路上にあるノードの値が(01101)だったならば、{受注ID，客先名，客先担当者，受注数，単価}のうち{客先名，客先担当者, 単価}からなるカラムの組を表現する葉ノードであることがわかります。

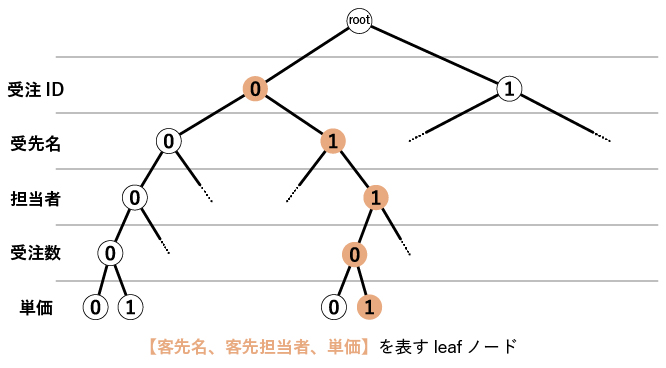
葉ノードに到達したら、そのノードの表すカラムの組が、レコードを一意に決めるかチェックします。 チェックの方法について、２通りの表現を考えてみました。

MySQLの記法に従う場合

テーブル名を{table}、カラムの組を{column 1}, {column 2}, …, {column n}で表現します。 下記コマンドの結果を用いることで、カラムの組がレコードを一意に定めるかどうか判定出来ます。

SELECT COUNT(DISTINCT {table}.{column 1}, {table}.{column 2}, …, {table}.{column n}) >= COUNT({table}.{column 1}, {table}.{column 2}, …, {table}.{column n}) FROM table

出力が1ならばレコードを一意に定めること、0ならば一意に定めないことがわかります。 ただし、既約であるかどうかは、１つのカラムの組に関する結果からは判定出来ないことに注意してください。 前述した通り、二分木を用いた探索を用いるならば、再帰的な関数で表現するのが筋の良い方法です。しかし、MySQLはそういった処理にあまり向かない（設計思想上望ましい操作とは言えない）ため、別の言語で書くことを想定して、アルゴリズムを疑似コードで表現してみましょう。

擬似コードで表現する場合

ここからは、一からアルゴリズムを設計していくことになります。少なからず数学的な表記を使うことになりますが、なるべく平易に説明をするよう努めますので、お付き合いください。

テーブルに含まれる全てのカラムの集合を$E$、その部分集合を$C$で表すことにします。このとき、$C \subseteq E$という関係が成り立ちます（$C$は$E$に含まれる）。 $E$には何通りの部分集合があるかというと、先ほどカラムの部分集合を(01101)のような２進数で表したことからもわかる通り、カラム数を$n$として$2^n$通りあります。これら$E$の全ての部分集合を$2^{E}$で表します（べき集合）。 $2^{E}$の要素が、$n$桁の２進数に１対１対応することに注意すると、この先の議論が解釈しやすくなります。

与えられたテーブルに含まれるレコードの集合を$R$とします。レコード数を$m$とする時、個々のレコードは$r_1, r_2, \dots, r_m \in R$と表すことが出来ます。 カラムの組$C$に対するレコード全体（テーブル）の射影を$R(C)$、個々のレコード$r_i$の射影を$r_i (C)$で表すこととします。ただし、射影された結果同一のレコードが生じる時も、両者を異なるものとして区別することに注意してください。 （MySQLでいうところの、DISTINCT指定しないSELECTコマンドに対応します。）

いま取り扱いたいのは、射影されたレコードの一意性が保たれるかどうか、ということです。あるカラムの組$C$を取り、射影されたレコードを上から順に見ていくとき、「既に見たレコード」の集合を$\widehat{R}(C)$で表します。いま手に取ったレコードが$\widehat{R}(C)$に含まれていないならば、その時点での一意性は担保されていることになります。

最後に、探索順序を制御する二分木について記法を決めておきます。まだ探索されていない葉ノードを$L$と表します。探索開始時は$L = 2^{E}$（すべてのカラムの集合が未探索）となり、探索するに従い$L$の要素が減っていきます。そして、$L = \emptyset$（空集合）となったとき、アルゴリズムは停止します。

これで擬似コードを記述する準備が出来ました。

全ての超キーを検出するアルゴリズム

超キーとは、レコードを一意に定めることのできるカラムの組を指します。 他にも幾つかの解釈がありますので、理解しやすいものを覚えておくと良いでしょう。

• 候補キーの２つの条件から既約性を取り除いたとき、該当するカラムの組の集合
• それ自体が候補キーであるか、または候補キーを含むようなカラムの組の集合

さて、候補キーのみを検出するアルゴリズムをいきなり記述してもよいのですが、既約であるという制約の表現が少し難しいです。 ですので、まずは既約の制約を気にしなくてもよいように、すべての超キーを検出するアルゴリズムを記述することにしましょう。

下記は、実装シーンを少し意識して、上記の擬似コードにコメントをつけたものです。

いくつか、実装の際の注意をしておきます。

二分木の実装

Step 1の以下の処理には、実際には二分木を活用することになります。

$L$というのは$n$桁の２進数の集合でしたから、二分木の葉ノードに対応しています。 二分木は、再帰的な関数（recursive function）として実装するのがセオリーです。再帰的な関数に階層を表すパラメータ$\mbox{floor}$を持たせ、$\mbox{floor} == n$となった時に得られた２進数についてStep 2を実行するのが、恐らくもっともシンプルな実装法です。

ハッシュの活用 - 計算量の最適化のために

上記の擬似コードはあくまで手続きの概要を示したものなので、実計算時間はもちろん、計算量にも効いてくる要素が曖昧になっていることに注意してください。 例えば、Step 3の以下の処理は、方法によって計算量が異なります。

この処理は、新規レコード$r_k(C)$が、既出レコード集合$\widehat{R}(C)$に含まれているかどうかを判定していますが、この処理にかかる時間は既出レコード集合のデータ構造に依存します。

例えば、既出レコード集合として配列を用いた場合、$r_k(c) \in \widehat{R}(c)$を判定する代表的な方法は線形走査(linear probing)です。その場合の計算量は、判定一回あたり$\mathcal{O}(|R|n)$となります。 一方、$\widehat{R}(c)$について適切なハッシュを用いて管理した場合、$r_k(C) \in \widehat{R}(C)$の判定は$\mathcal{O}(n)$で行うことができます。

本題：全ての候補キーを検出するアルゴリズム

さて、いよいよ全ての候補キーを検出するアルゴリズムに入りましょう。

この場合の難しさは、既約性の判定も行わなければならないという点です。 一つの素朴なアイデアとして、前述のアルゴリズムのStep 3に「既約性の判定」を入れるというものが考えられます。

このとき、既約性の判定は、具体的にどのような手続きで行うべきでしょうか。 カラムの集合$C$が既約であるためには、「$C$の全ての部分集合」が、レコードを一意に特定出来ないものである必要があります。 ところが、その判定には困難が伴います。

• 一般に$C$の部分集合は要素数の指数オーダ存在する
• 先のアルゴリズムでは$C$を取る順番については言及しなかったので、$C$の部分集合$C’ (\subset C)$についてはまだ未探索かもしれず、候補キーであるかわからないケースがある

よって、Step 3を書き換えるアプローチはあまり好ましくありません。

ではどうすればよいかと言うと、実は判定対象を決定するStep 1を書き換えると、効率的に既約性の判定が行えます。

上記の擬似コードは、Step 1をサブステップに分け、幾つかの処理を追加したものになっています。 変更点についてコメントしたものが下記の擬似コードです。

まずStep 1-1の「任意の未探索葉ノード$C’$を含まない$C$を取る」という語義を説明します。 例えばアルゴリズム開始時は、二分木のすべての葉ノードは未探索です（$L = 2^E$）。このような時、上記の制約にしたがって取りうる葉ノードとしては、($0000\dots0$)のみとなります。 なぜなら、$1$を1つでも含む葉ノード$C$は、必ず空集合$(0000\dots0)$を含んでしまうためです。

空集合の次に取るべき葉ノードは、$1$を１つだけ含む葉ノードです。仮に$1$を２つ以上含む葉ノードを取ったとすると、$1$を１つだけ含む葉ノードを含んでしまうでしょう。

以降も同様に、未探索のノードを含んでしまわないように探索を進めていきます。

そのような処理は難しそうだな、と思われたかもしれませんが、実は上記の制約を満たすよう二分木を探索することは簡単です。 その方法とは、「各ノードにおいて0/1を選択する際、0を先に選択する」よう実装することです。このように実装したならば、任意の未探索葉ノード$C’$を含まないような葉ノードに必ず行き着くのですが、興味があればぜひ、その証明を考えてみてくださいね。

そして、Step 1-2では、これまでに得られた候補キーの集合$\widehat{R}(C)$の中に、$C$に含まれるようなカラムの集合$C’$があるかどうかを判定しています。もしあるならば、$C$が既約でない超キーであることは明らかです（本記事の既約の定義、及び超キーの定義2.を参照）。既約でない超キーについては出力に含めるべきではないので、その時点でStep 1-1に戻ることが正当化されます。

Step 1-1, 1-2を加えたおかげで、Step 3に一切の変更を加えることなく、あるカラムの組$C$が候補キーであることを確信できます。

なぜなら、それが候補キーではない超キーであるような場合は、Step 1-2の段階で判定対象から除外されていたはずだからです。

判定対象除外の実装テクニック - 二分木の枝刈り

Step 1-2で行う、判定対象除外の実装時に役立ち、計算時間を大幅に改善できるテクニックとして「枝刈り」を紹介します。ナップサック問題などの最適化問題を解く際にも使われるテクニックで、覚えておくと使えるタイミングがあるかもしれません。

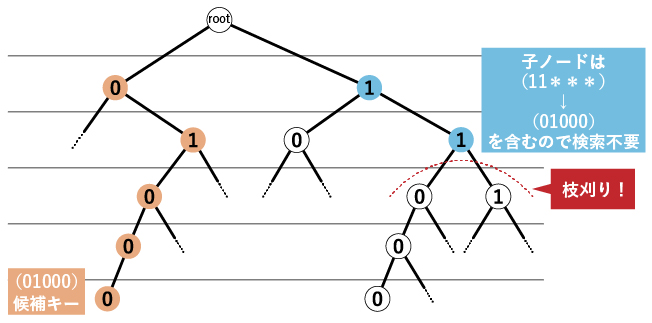
二分木の探索中に、葉ノードではないノード$S$にいたとします。そのノードが表す値を、$(11\ast\ast\ast)$のように、まだ未定の部分は$\ast$を使って表現することにします。 この時、ある候補キー$K \in L^*$が存在して、$S$が$K$を（対応するカラム集合の意味で）含むならば、$S$自身及び$S$の子ノードは既約でない超キーを表すことがわかります。

より正確に書くと、２進数で表現した$S, K$の$i$桁目をそれぞれ$S_i, K_i$で表したとき、以下の条件を満たす$S$が$K$を含む超キーと言えます。

• $S_i \neq \ast$ならば$S_i \geq K_i$
• $S_i = \ast$ならば$K_i = 0$

超キーは候補キーではありませんので、そこから先の探索を行う必要がなく、処理を削減できます。 このような、目的に基づく条件判定と処理削減のテクニックを「枝刈り」と呼びます。適切な枝刈りは、プログラムの正当性を損なわずに処理速度を向上させることが出来ます。

課題：計算量はさらに改善可能か？

さて、枝刈りを導入した際の計算時間ですが、効率的ではあるものの、依然として指数時間かかってしまうように見えます。果たして、多項式時間で候補キーを検出する方法はないのでしょうか？

• あるとしたら、それはどんな方法？
• ないとしたら、どうやって証明できる？

上記も興味深いテーマではありますが、本記事では問の設定に止めておきます。 指数時間・多項式時間アルゴリズムを区別する「計算量理論」の入門書としては、下記の書籍などが挙げられます。上記の問について取り組みたいが、計算量理論の知識がない、という方向けの入門にはお勧めです。

• 杉原 厚吉，「データ構造とアルゴリズム」，共立出版，2001．

また、「問題を解く多項式時間アルゴリズムが存在しないことの証明」には、よく「NP困難性の証明」が用いられます。そちらについてあまり数学を使わずに学びたい方には、以下の書籍がお勧めです。

• 岩田 茂樹，「NP完全問題入門」，共立出版，1995．

以上が、単一テーブルから全ての候補キーを検出するアルゴリズムの構築とその紹介でした。次回は、このアルゴリズムで得られた候補キー集合を参照し、ボイスコッド正規形（BCNF）を得る方法について考えていきたいと思います。