本記事は、Python上で動作するニューラルネットワークのライブラリ「Chainer」を使ってマルコフ連鎖を実装、様々な実験を行うものです。 マルコフ連鎖に関する基礎的な解説もしていくので、初学者の方もご安心ください。
ChainerとMarkov chain
Chainerはそもそもがニューラルネットワークの実装のために開発されたライブラリです。一方、マルコフ連鎖はChainと名前が付くものの、Chainer及びニューラルネットワークに直接の関係はないことに注意してください。ニューラルネットワークは1940年代に起源のあるモデルですが（注目され始めたのは21世紀に入ってからです）、マルコフ連鎖は1906年に最初の論文が発表されている、より古典的かつシンプルなモデルです。
では、本来関係のない両者を結びつけることでどんなメリットが得られるのでしょうか？
Chainerを学びたい人にとっての「良さ」
Chainerでマルコフ連鎖を書こうという試みの長所は、ニューラルネットワークの知識がなくてもChainerを使った記述や動作（の一部）を理解でき、しかもそれなりに意味のある分析ができるというところです。 とりあえずChainerを触ってみたい、という方に本記事の内容はおすすめです。
マルコフ連鎖を学びたい人にとっての「良さ」
Chainerはマルコフ連鎖のためのライブラリではないのですが（だからこそ）、一からコードを書きながらロジックを理解していくことができるという点で優れています。
マルコフ連鎖はとてもシンプルなモデルなので、内部のロジックを一からコーディングしていくことは難しくないのですが、冗長になりがちです。Chainerは行列演算と勾配計算をサポートしていますので、実装の冗長さをうまく取り除いてくれます。その意味で、エンジニアがマルコフ連鎖を「作りながら学ぶ」には非常に向いた環境だと感じています。
前置き
Python (numpy)の便利さ
Chainerに限らず、Python (numpy)は行列演算がサポートされており、高校〜大学の数学で習う行列同士の掛け算などを自分で実装しなくて良い手軽さがあります。これはChainer以前に、Python (numpy)の便利さです。 Chainerを用いることの更なる利点については、マルコフ連鎖として定義できる現象の実例を挙げてからの方が紹介しやすいため、おいおい述べたいと思います。
Chainer tutorialとの対応
本記事は、下記ページ「Introduction to Chainer」における、「Optimizer」の手前までの内容をカバーします。
「Optimizer」以降を読み進めるにはニューラルネットワーク（特に、確率的勾配降下法と損失関数）の知識が不可欠になるので、別途専門書を読む必要があります。逆に言うと、そこまでの内容を読むのにニューラルネットワークの知識は必須ではありません。（挙動を解釈しづらい部分があるので、知識がないとハマることはありますが…。例えば、f.W.gradの出力内容など。） 本記事は、ニューラルネットワークの知識なしで読み書きできる範囲で、Chainerを使って意味のある「結果」を導くことをゴールとします。
マルコフ連鎖の定義と、ニューラルネットワークとの関係
一応、マルコフ連鎖の一般的な説明を最初にしておきましょう。 マルコフ連鎖は行列で表される固定的な遷移規則によって、ネットワークの逐次的な状態変化を記述し、その性質から何らかのアウトプットを得ることを目的に使われる数理モデルです。 まずは例を用いて「利用例」を紹介してみたいと思います。後述する実装パートでは、ここで説明する例の実装を試みます。
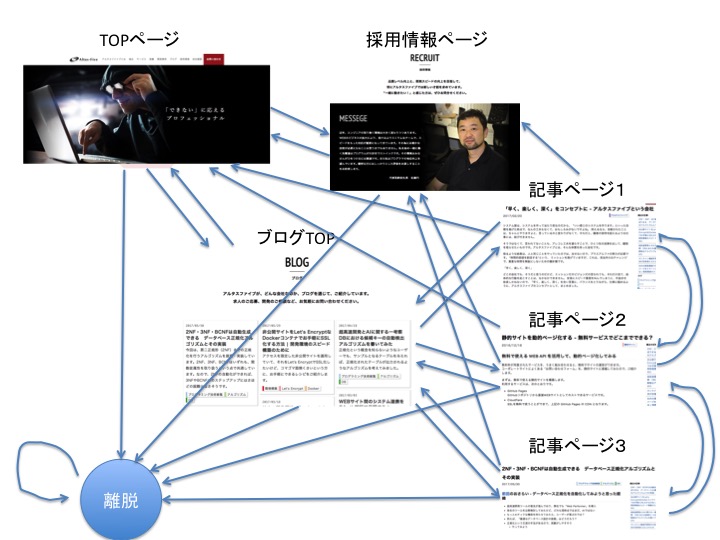
上図に示したのは、当サイトの遷移図（一部）です。説明の簡単化のため、下記ページしか存在しない構成になっています。
- TOPページ
- 採用情報ページ
- ブログTOP
- 記事ページ1,2,3
枝（矢印）はリンクの有無を表しています。また、「離脱」というのはサイト外へ遷移したユーザーの状態を表し、データ上は他のページと同様に扱うものとします。 この図は、サイト上のユーザーの移動を抽象化したものと捉えることができますね。 マルコフ連鎖の文脈では、それぞれのページを 状態 と呼び、状態から状態へ移ることを 遷移 と呼びます。
「状態」という用語に関する注意
例を用いてマルコフ連鎖の説明をするとき、ページを「状態」と呼ばねばならないことにしばしば違和感が生じます。（今回の例も、そうであるかもしれません。） マルコフ連鎖はネットワーク上を動く主体、つまり「ユーザー」の振る舞いを分析するためのツールです。なので各ページが抽象的に表しているのはページそのものというより「あるユーザーがそのページを見ているという状態」だと考えてください。
マルコフ連鎖の応用例
マルコフ連鎖は、このような ネットワーク（有向グラフ） を定義したとき、状態がどのように動くかを分析することのできる簡便かつ強力なツールなのです。 今回はサイト上のユーザー遷移を例にとりますが、応用例は多岐に渡ります。
| トピック | 状態 | 遷移の例 |
|---|---|---|
| 天気予報 | 天気（晴、曇り、雨、雪、etc.） | 晴れ の翌日が 雨 |
| 人口移動 | 市区町村（新宿区、千代田区、港区、渋谷区、etc.） | 新宿区 在住者が 渋谷区 に引っ越し |
| Webサイトのユーザー遷移（今回のトピック） | ページ | TOPページ から ブログTOP へ遷移 |
| 自然言語処理 | 単語（我輩、猫、名前、ミケ、etc.） | 我輩 という単語の次に 猫 という単語が来る |
システム開発者にとって興味ある例は、今回扱うユーザー遷移や、自然言語処理でしょう。ただし、マルコフ連鎖を使った自然言語処理（文章の自動生成）はニューラルネットワークを用いたアプリケーションのように高い精度を持つわけではなく、「人口無脳」と表現されるレベルのものであることを注意しておきます。この後説明するように、マルコフ連鎖は状態から状態への推移確率を確定的に定義するため、人間の脳が行うような高度な処理には本来向きません。
マルコフ連鎖を用いた自然言語処理ライブラリには下記のものなどがあります。手軽に試すことができますので、興味のある方は触ってみてください。
マルコフ連鎖とユーザー遷移
マルコフ連鎖のイメージを掴んでもらうため、まずはユーザーの遷移についてデモンストレーションをしてみます。
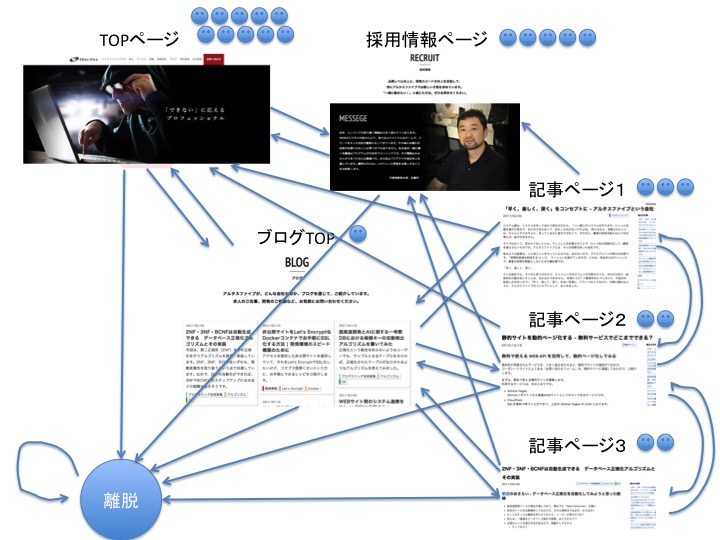
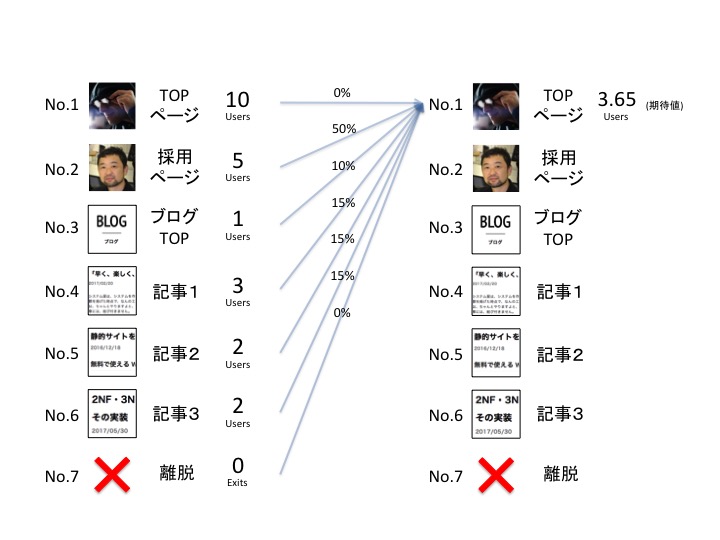
上図に表したのは、サイトの各ページに着地（Googleなどの外部ページから遷移）してくれたユーザーの数です。これらのユーザーがリンクを辿って、どのように遷移していくかを実験してみましょう。
そこで重要になるのが、ユーザーがどんな規則性を持ってページ間を遷移しているか、ということです。 遷移の規則性も議論の種にはなりえますが、ここではシンプルに「今いるページ（状態）によって確率的に決まる」と考えることにしましょう。例えばTOPページにいるユーザーについて、以下のように確率分布しているとします。
- 採用情報ページに遷移するユーザーが 50%
- ブログTOPに遷移するユーザーが 30%
- 離脱するユーザーが 20%
- その他のページに遷移するユーザーはいない
これら「あるページから、別のページへ遷移する確率」を総称して 推移確率 と呼びます。マルコフ連鎖の分析においては、手元に推移確率のデータが必要となります。 確率を扱うときは「期待値」を使って説明するのが常道なのですが、小数が出現して話が煩雑になります。まずは「遷移のイメージ」だけを掴んで頂きたいので、モデルから算出される期待値のことはさておき、「実際の移動経路（例）」を図示することにします。
では早速、上図の状態から全ユーザーを一斉に「えいやっ」と遷移させて見ましょう。その結果が下図です。
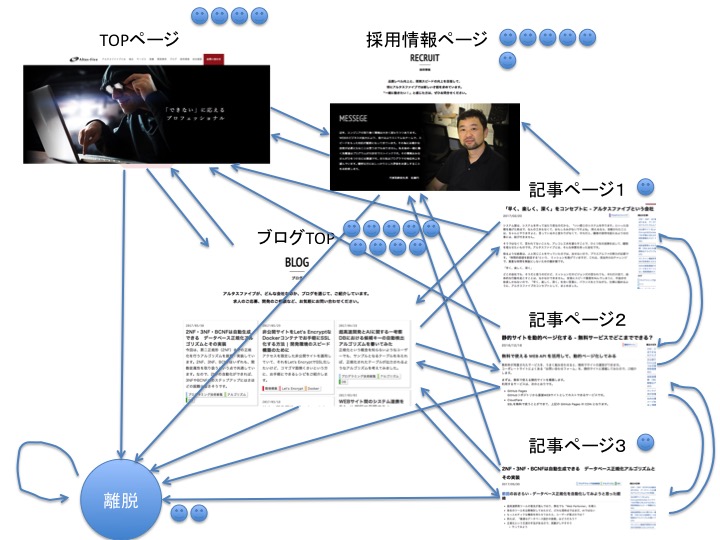
所感
- ブログTOPに多くのユーザーが集まった
- ２人のユーザーが離脱してしまった
ではさらにもう一度移動させるとどうなるかを見てみます。
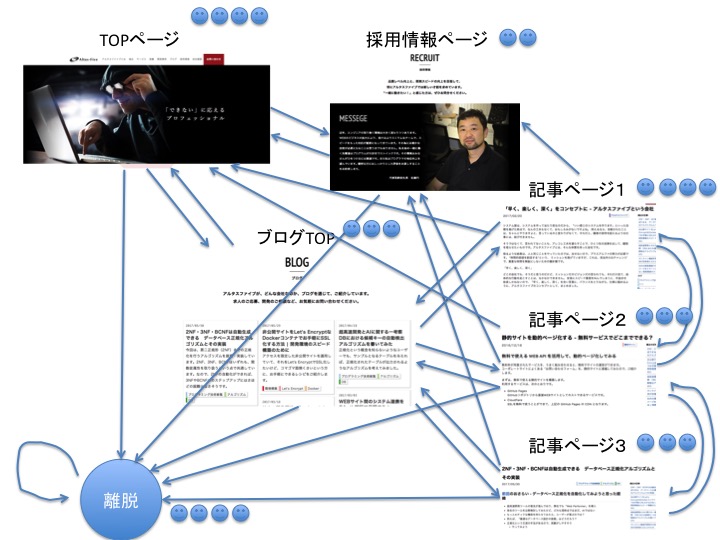
所感
- 各記事ページに多くのユーザーが集まった
- １つ前のステップにおいて、たくさんのユーザーがブログTOPを見ていたためと考えられる
- ２人のユーザーが新たに離脱してしまった
こんな具合にユーザーを何度も遷移させて、どのような振る舞いをするか調べるのがマルコフ連鎖を用いた分析です。
マルコフ連鎖の推移確率行列
本節では、上述したユーザーの遷移をシステム上で取り扱うにはどうすれば良いか、という話をします。 まずは、ネットワークの性質をデータとして保持する必要がありますが、まずは推移確率をコンパクトにまとめることを試みましょう。
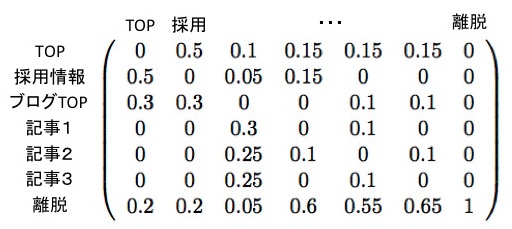
上図の見かたを説明します。各行・各列は状態（ページ）に対応しており、各セルに含まれる数値は「数値が含まれる列の状態から、行の状態に遷移する確率」を表しています。
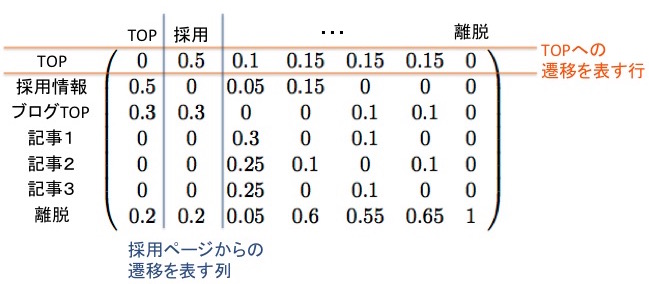
例えば(TOPの行, 採用の列)にある成分が0.5であることは、「採用情報ページからTOPページに遷移する確率が0.5(50%)」であることを表しています。
この推移確率をコンパクトにまとめた表は数学（線形代数）の文脈で「行列」(Matrix)と呼ばれるもので、データ上は２次元リストなどを用いて表します。 行列は加・減・乗算といった演算の定義があり、マルコフ連鎖やニューラルネットワークの学習においては特に乗算（掛け算）の定義を知っていることが 必須 です。 実は、マルコフ連鎖における「乗算」は直感的な解釈ができるので、行列演算が苦手な方の克服材料としても使うことができます。ですのでもし、抵抗感があっても読み進めてみてください。
行列同士の乗算を定義する
まず書き方ですが、二つの行列を並べることによって「積」（乗算結果）を表します。
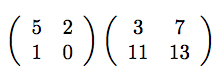
$2\times2$行列同士の積を書いてみました。計算結果はどのようになるでしょうか。
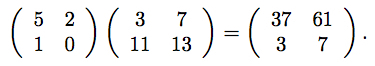
このようになります。行列同士の乗算の計算過程について、おさらいしておきましょう。
計算結果の(1行目, 1列目)の成分を計算する方法を説明します（以降、(1, 1)成分と略記）。 (1, 1)成分を求めるには、乗算の左オペランドの１行目と、右オペランドの１列目を使います。左オペランドは左から右、右オペランドは上から下に数値を見て、それぞれ対応する位置にある数値の積について総和を取ったものが計算結果になります。
一般に、($i, j$)成分を計算するには、左オペランドの$i$行目と、右オペランドの$j$行目を見て、同様の計算を行います。
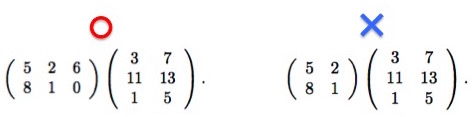
このことからわかる通り、左オペランドの 列数 と右オペランドの 行数 が一致している時のみ、行列の積は定義されます。上図の右のケースでは不一致が生じているため、計算結果は未定義となります。
マルコフ連鎖の遷移は、行列同士の乗算で表現できる
上記の行列の乗算は、マルコフ連鎖の「遷移」という概念と面白いようにハマります。下記の、少し大きな行列の乗算をご覧ください。
この行列演算が、何を意図したものであるかについてご説明します。
左辺（イコールの左側）の解説
左辺の左オペランドの$7\times7$行列は、先ほど例示したWebサイトのユーザー遷移に関する推移確率行列になっています。右オペランドの$7 \times 1$行列（7次のベクトル, vector）は、やはり先ほど例示した各状態（ページ）に着地したユーザーの数になっています。マルコフ連鎖の文脈では、これを 分布 とも呼びます。
右辺（イコールの右側）の解説
推移確率行列と分布を乗ずることで求まる右辺の計算結果は、$7\times1$行列になります。（先ほど紹介した乗算の手続きから、一般に$l\times m$行列と$m \times n$行列の積は$l \times n$行列になります。） ここで右辺のもつ意味を明らかにするため、もう一度乗算の計算過程についておさらいしてみましょう。
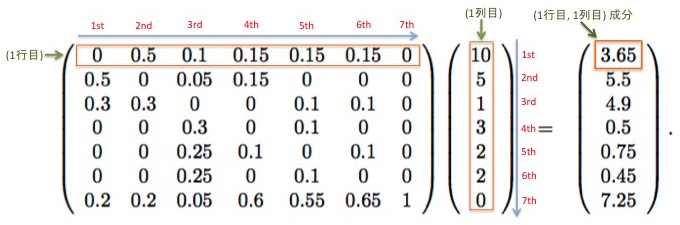
積の(1, 1)成分を求めるには、左オペランドの１行目と右オペランドの１列目（今回は１列しかないので、行列全体）を見るのでした。そして、ポジション（1st, 2nd, 3rd, ...）が対応する数値同士の積の総和を取ります。(1, 1)成分を求める具体的な計算式は下記のようになります。
$0 \times 10 + 0.5 \times 5 + 0.1 \times 1 + 0.15 \times 3 + 0.15 \times 2 + 0.25 \times 2 + 0 \times 0 = 3.65$
ここで、推移確率行列の要素が持つ意味をおさらいしておきましょう。$(i, j)$成分は「状態$j$から状態$i$へと遷移する確率」を意味するものでした。例えば推移確率行列の$(1, 2)$成分である$0.5$は、「第２ページ（採用情報）にいるユーザーが、直後に第１ページ（TOP）へと推移する確率が50%」であることを示します。 そして右オペランドは「状態上の分布」を表すものです。右オペランドの$(2, 1)$成分は$5$ですが、これは「第２ページにいま５人のユーザーがいる」ことを表します。 右オペランドの$(1, 1)$成分の計算において、この$5$に対してマッチングされる値は$0.5$(50%)です。計算結果は$5 \times 0.5 = 2.5$となりますが、これは「５人のユーザーが第２ページにおり、うち0.5(50%)のユーザーが第１ページに遷移するので、第２ページから第１ページへ遷移するユーザーは（期待値の意味で）2.5人いる」という風に書き下すことができます。 以上の数値同士の乗算を、1stから7thまですべてのポジションについて行った総和である数値$3.65$は何を表すでしょうか？
考えやすくするために、$(1, 1)$成分の計算を図示してみました。
上図と、下記の計算式を照らし合わせてみてください。
$0 \times 10 + 0.5 \times 5 + 0.1 \times 1 + 0.15 \times 3 + 0.15 \times 2 + 0.25 \times 2 + 0 \times 0 = 3.65$
これは、「遷移後に第１ページにいるユーザー数の期待値」の計算になっていることが分かります。第１ページへの遷移は第１〜第７全てのページから起こりえますが、全ての「遷移元」に関して遷移数の期待値の合計を取る計算になっているわけですね。
右オペランドの他の成分についても同様で、$(i ,1)$成分（上から$i$番目の成分）は、「遷移後に第$i$ページにいるユーザー数の期待値」になっています。
つまり 分布のベクトルに対して左から推移確率行列を掛けると、遷移した後の分布が求まる のですね。
マルコフ連鎖とページランク
このモデルを用いる際に注意せねばならないことは、 「現在の状態」のみに依存して次の状態への推移確率が決まる という仮定を置いているということです。これは非常に強い仮定であり、いま分析したい対象に当てはまるかどうかはよく吟味せねばなりません。ユーザー遷移の分析で言えば「ユーザーの性別・年齢・興味といった属性を無視してよいのか？」「２つ以上前に見ていたページも考慮すべきでは？」などの疑問が湧き、これらの影響が無視できないならばモデルを適宜改良する必要があります。
ここで、マルコフ連鎖をWebのユーザー遷移の分析に適用することについては、偉大な先例があることに言及させてください。Googleの創業者の一人であるラリー・ペイジが提案した「ページランク」は、マルコフ連鎖に基づくモデルなのです。 下記のペイジの論文を読むとわかる通り、ページランクの仕組みは上述した内容とほぼ同一のロジックによって、Webページの価値を評価するというものでした。Googleの登場当時は、このモデルが革新的なロジックとして受け入れられたという訳です。 （明示的に「Markov chain」という文言は出てきませんが、下記論文のpp.3-5にある図はマルコフ連鎖の概念図そのものです。）
ただし、ページランクには「人工的なリンクによる評価の操作ができる」という弱点がありました。その対策のために検索エンジンがアップデートされ（ペンギンアップデート）、その後ページランクはGoogleの検索エンジンから脱落していきます。 マルコフ連鎖による単純なモデリングは、残念ながら検索エンジンとしては欠点がありましたが、データを取り扱うフレームワークとしてはいまも十分に有効です。
ニューラルネットワークの順伝播との類似性
※この節は読まなくても、理解上差し支えありません。
ニューラルネットワークを齧ったことのある方は、大抵の文献に直上の挿絵とよく似た図が入っているのをご存知かと思います。例えば、ニューラルネットワークの入門書としてよく引用されている下記文献の、p.2やp.9などです。
ニューラルネットワークは層間の順伝播を線形式で行うことが一般的ですが、これはマルコフ連鎖における「推移確率行列を左から掛ける」という操作と全く同じ計算です。 ここに両者の類似性があるのです。
まったくの初学者がニューラルネットワークを学ぶにあたっては、少し寄り道にはなりますが、マルコフ連鎖について知っておくと、様々なシーンにおいて理解の助けになると考えています。
（繰り返しになりますが、マルコフ連鎖の基礎理解に必要な知識は、ニューラルネットワークの理解に必要な知識の一部分となっています。）
Chainerでマルコフ連鎖を実装してみる
いよいよ、Chainerを使ったマルコフ連鎖の実装に移ります。Chainerの公式情報としては、下記のTutorialを参照すれば十分ですので、ご活用ください。
また、開発環境の導入については下記ガイドをご覧ください。
ChainerはPythonの数値計算ライブラリであるnumpyを活用しています。numpyは上述した行列の演算をnp.ndarrayというクラスでサポートしているため、行列積や、より高度な計算を関数として呼び出すことが出来て便利です。 以降は開発環境の導入は済んだものとして、iPythonのような対話型環境を用いるか、.pyファイルに手続きを記述していく前提で話を進めます。
ChainerのVariableを定義する（分布）
まずはマルコフ連鎖の「分布」を定義してみる事にしましょう。$n$通りの状態の上の分布は$n \times 1$行列で表されますが、これをndarrayクラスのオブジェクトとして定義します。
np.array([[10, 5, 1, 3, 2, 2, 0]])
ndarrayクラスのオブジェクトを生成するには、np.array関数を用いるのが一般的です。引数としてPythonのリスト（行列なので二次元リスト）を渡せば、対応する行列が生成され、行列和・積の計算や、より高度な計算（逆行列の計算や、固有値・固有ベクトルの計算）を関数として呼び出せるようになります。
Chainerにおいてはndarrayクラスのオブジェクトをそのまま扱わずに、ndarrayを入力としてVariableオブジェクトを生成します。これを踏まえ、Chainerの計算で用いる分布は下記のように定義します。
distribution = Variable(np.array([[10, 5, 1, 3, 2, 2, 0]], dtype=np.float32))
ここで、distributionは所与の変数名です（分布の意）。 Variableクラスのコンストラクタの引数として渡せるものは、numpy.ndarray又はcuda.ndarrayオブジェクトです。 データタイプはTutorialに倣い、numpyの32ビット浮動小数点型であるnp.float32を指定しています。
ChainerのLinkを定義する（遷移を制御するクラス）
次に推移確率行列を定義しますが、これにはChainerのLinkというオブジェクトを用います。Linkの主な機能は以下の通りです。
- $m$次元ベクトル（の集合）を$n$次元ベクトル（の集合）へと変換するメソッドを持つ
- 変換の内容を決めるパラメータを保持している
- Linkを組み合わせてネットワークを構築し、誤差関数を定義して訓練データを与えることで、パラメータの数値を最適化できる（ニューラルネットワーク向きの機能。今回は触れない）
Tutorialでは特によく用いられるLinkとしてL.Linear（線形リンク）を紹介しています。L.Linearは「行列の積と和だけで表現できる変換」をカバーしていますので、今回の遷移という用途にはぴったりです。早速定義してみましょう。
transition = L.Linear(7, 7)
transitionは所与の変数名で（遷移の意）、L.LinearはL.Linearのコンストラクタです。(7, 7)という引数は、「7次元から7次元への変換を行うLinkを定義」するよう指定しています。 この定義により、transitionは「７という次元数（状態数）は変えずに、各次元に対応する数値を変えたものを返すL.Linear」となります。 今は７状態からなるネットワークについてマルコフ連鎖を実装しようとしていますので、Linkには「分布を入力すると、遷移後の分布を返してくれる」機能が求められます。なので、入力と出力の次元数が等しいLinkを定義しました。 問題は、このリンクの行う処理の中身です。 transitionについて、推移確率行列にあたるパラメータはtransition.W.dataに格納されていますので、これを確認してみましょう。
print transition.W.data
>>> [[-0.86491805 -0.16170089 0.34361446 -0.0636134 -0.22656611 -0.63621569 -0.17878614]
>>> [ 0.17760617 0.29629865 -0.33722615 -0.12503195 0.16237867 -0.20694737 -0.60708505]
>>> [-0.06904662 -0.03128463 0.22083846 0.36412853 -0.03627913 -0.03684266 0.54450828]
>>> [ 0.10557969 0.04198727 -0.01530487 0.61610317 -0.16425815 -0.26798156 0.26575172]
>>> [-0.0686424 -0.54063159 -0.34978956 0.24700937 -0.16933322 -0.04976032 -0.21227303]
>>> [ 0.57017905 -0.00309141 -0.00351088 0.2253985 -0.01208178 -0.11499751 -0.2914691 ]
>>> [-0.40216371 0.69113183 -0.45077264 0.32903543 0.16823213 -0.36826468 0.29529756]]
このように、生成時にはランダムなパラメータが入力されています。これを意図した値にするためには、transition.W.dataに代入を行うか、コンストラクタの引数としてnp.ndarrayオブジェクトを渡します。
ここでは代入を行うことで対応することにしましょう。
transition.W.data = np.array([[0, 0.5, 0.1, 0.15, 0.15, 0.15, 0],
[0.5, 0, 0.05, 0.15, 0, 0, 0],
[0.3, 0.3, 0, 0, 0.1, 0.1, 0],
[0, 0, 0.3, 0, 0.1, 0, 0],
[0, 0, 0.25, 0.1, 0, 0.1, 0],
[0, 0, 0.25, 0, 0.1, 0, 0],
[0.2, 0.2, 0.05, 0.6, 0.55, 0.65, 1]], dtype=np.float32)
（もうひとつ、transition.bというパラメータがあるのですが、これは0によって初期化されるため以降の計算に影響しません。今回は説明を省略します。）
以上の定義に基づき、distributionの状態から、transition.Wで指定の推移確率行列に基づいて遷移したユーザーの分布を求めてみましょう。
distribution_after_transition = transition(distribution)
print distribution_after_transition
>>> variable([[ 3.65 5.5 4.9 0.5 0.75 0.45 7.25 ]])
想定通りの結果となりました（ただし、実際にはnp.float32由来の誤差が僅かに生じます）。Chainerでは各クラスに__call__関数が定義されており、オブジェクト名によって基本的な関数を呼び出すことが出来ます。L.Linearオブジェクトの場合、入力をWに基づいて変換したものを返す関数が呼び出されます。
Chainクラスを用いてMarkovChainを定義する
ChainerにはChainというクラスがあり、Chainオブジェクトのインスタンス変数としてLinkを配下に置くことで、様々な機能を使うことが出来ます。 Chainはニューラルネットワークの構築を主眼に置いたクラスですが、先述した通りニューラルネットワークとマルコフ連鎖には類似性があるため、Chainクラスを使ってMarkov Chainを定義することは容易です。
class MyMarkovChain(Chain):
def __init__(self, tpa):
super(MyMarkovChain, self).__init__()
if tpa.shape[0] == tpa.shape[1]:
dim = tpa.shape[0]
with self.init_scope():
self.transit = L.Linear(dim, dim)
self.transit.W.data = tpa
self.loop = 0
def __call__(self, dist):
return self.transit(dist)
MyMarkovChainクラスを、Chainクラスを継承して定義しています。コンストラクタにnp.ndarrayクラスの引数tpm（transition probability matrix, 推移確率行列の意）を渡すと、行と列の次数が等しいことを確認した上で、インスタンス変数であるL.Linear型変数self.transitに格納します。また、以降のloop回数制御のため、self.loopというインスタンス変数も用意しておきます。 このクラスを用いるには、例えば以下のようなコードを書きます。
markov_chain = MyMarkovChain(np.array([[0, 0, 0.1, 0.15, 0.15, 0.15, 0],
[0.5, 1, 0.05, 0.15, 0, 0, 0],
[0.3, 0, 0, 0, 0.1, 0.1, 0],
[0, 0, 0.3, 0, 0.1, 0, 0],
[0, 0, 0.25, 0.1, 0, 0.1, 0],
[0, 0, 0.25, 0, 0.1, 0, 0],
[0.2, 0, 0.05, 0.6, 0.55, 0.65, 1]], dtype=np.float32))
distribution = Variable(np.array([[10, 5, 1, 3, 2, 2, 0]], dtype=np.float32))
print markov_chain(distribution)
1行目では推移確率行列を与えることで、MyMarkovChainクラスのmarkov_chainを定義しています。 2行目で初期分布 distributionを定義し、3行目ではdistributionから一回だけ遷移させた結果の分布を計算し、出力します。（markov_chainクラスについて関数名を明示せず関数呼び出しをしているので、 call メソッドが呼び出されます。）
このクラスに対し、さらにクラスメソッドを定義してみましょう。
指定の回数だけ遷移させる関数
引数timesを取り、times回遷移させる関数transit_designated_timesを書いてみましょう。 マルコフ連鎖における複数回遷移は明快で、初期分布を表すベクトルに対し、左から times回、推移確率行列を掛けてあげるだけです。
def transit_designated_times(self, dist, times):
temp = dist
for num in range(times):
temp = self(temp)
return temp
計算量を減らす工夫
一般に、$n \times n$行列と$n \times 1$行列の掛け算の計算量は$\mathcal{O} (n^2)$です。推移確率行列を左から$t$回掛ける愚直なやり方だと、$\mathcal{O} (tn^2)$の計算量がかかることになりますが、これを短縮する方法があります。
一般に推移確率行列を$A$、分布を表すベクトルを${\bf d}$と表した時、左から$A$を$t$回掛ける操作は$AAA \dots A{\bf d}$のように表されます（$A$が$t$個。）これを通常の値（スカラ）の累乗と同じように$A^t{\bf d}$と表します。 行列の計算には結合則というものが成り立つことが知られており、${\bf d}$に対して$A$を左から$t$回掛けても、$A^t$を先に求めてから${\bf d}$に掛けても、計算結果は変わりません。言い換えると、$A$に従う$t$回の遷移を表す$A^t$という推移確率行列が存在するので、それを先に求めてから${\bf d}$に掛けるやり方でも良いのです。
そして、$A^t$には効率的な求め方があるのでご紹介します。ここでは$A^{10}$を求めることにしましょう。
- $A$と$A$を掛けて$A^2$を求め、記憶
- $A^2$と$A^2$を掛けて$A^4$を求め、記憶
- $A^4$と$A^4$を掛けて$A^8$を求め、記憶
- 記憶していた$A^2$と$A^8$を掛けて$A^{10}$を作る
最後の4.で掛けるべき要素は、一般に、$t$の二進数表現に基づいて決めることになります。 この方法を用いれば、計算量は$\mathcal{O} (\log t n^2)$のオーダまで落ちることが知られています。
定常分布（極限分布）まで遷移させる関数
マルコフ連鎖には定常分布(Stationary distribution)と呼ばれる分布が存在することがあります。
推移確率行列を$A$、分布を$\pi$として、$A\pi = \pi$となるような分布として定義されます。つまり、遷移させても分布（の期待値）が変化しないような分布$\pi$を定常分布と呼ぶわけです。
ちなみに今回取り上げている推移確率行列については自明で、$n$人のユーザーからなる分布については$(0, 0, 0, 0, 0, 0, n)$が唯一の定常分布です（全員が離脱した状態）。推移確率行列の取り方によっては、複数状態に遍在したり、定常分布が複数存在したり、定常分布が存在しないこともあります。（詳しくはマルコフ連鎖のテキストをご参照ください。）
定常分布には「一旦そこに入り込むと出られない」という性質だけでなく、「別の分布を何回も遷移させていると、定常分布にだんだん近づいていく」という性質を持つことがあります。今回の推移確率行列は「いかなる分布であっても、遷移を十分な回数行うと、定常分布に収束する」という強い性質があります。（このような定常分布を特に、極限分布と呼びます。）
という訳で、極限分布まで遷移させる関数を書いてみましょう。先のサイト内遷移の例でいうと、この関数を定義するメリットは以下の通りです：
- 各ページへの訪問数に基づいてユーザーの動きを予測し、各ページおよび全体のページビュー数や、ユーザーあたりの平均ページビュー数を概算できる
ひとまず、「遷移させても分布が変わらなくなるまで遷移させ続ける」という愚直な方法で書いてみようと思います。
def transit_until_limit_distribution(self, dist_before_transit):
self.loop = self.loop + 1
dist_after_transit = self(dist_before_transit)
print "Distribution after", self.loop,"th transition:"
print dist_after_transit
if np.linalg.norm(dist_after_transit.data - dist_before_transit.data) < (10 ** -5):
self.loop = 0
return dist_after_transit
else:
return self.transit_until_limit_distribution(dist_after_transit)
transit_until_limit_distributionは再帰的な関数として書きました。else文の中で自身を呼び出していますので、if文の中身がFalseである限り関数が繰り返し呼び出されます。 ここでif文の不等式について解説しておきましょう。 np.linalg.normは、ベクトルのノルムと呼ばれる数値を計算する、numpyの関数です。ノルムはベクトルに対して「長さ」や「大きさ」といった尺度を与えるもので、２次元や３次元の「距離」を拡張した概念です。 np.linalg.normの引数としてdist_after_transit.data - dist_before_transit.dataを渡しています。「遷移後の分布」と「遷移までの分布」が近づいていくと、その差のベクトルはきわめて小さくなるため、距離であるノルムは0に近づいていきます。ノルムが$10^-5$という「十分小さい値」を下回った時点で計算を打ち切るようにして、近似的に定常分布を求めています。
より望ましい計算方法
上記のコードは「定常分布」の観念的な説明も兼ねているため、あえて非効率な計算方法を取っています。上記のコードには幾つかの弱点があります：
- 計算量が大きい（状態数を$n$、ループ回数を$l$として$\mathcal{O} (ln^3)$）
- 定常分布に近づかないような初期状態を選ぶと、無限ループに陥る
- あくまで近似的な計算である
ここでは、より望ましい計算方法として「固有値１に対応する固有ベクトルを求める」という方法があることにのみ言及しておきます。 固有ベクトルの計算についてもnumpyの関数として実装されています。理論にご興味のある方は、線形代数の入門書をご参照ください。
感度分析を行うMyMarkovChainクラスを書いてみる
さて、ここまでの内容だけですと「Chainer使わなくてもnumpyで簡単に出来るじゃん」というツッコミが入りそうなので、そろそろChainerならではの要素を盛り込んでみたいと思います。
ニューラルネットワークライブラリとしてのChainerの強みとしては、以下が挙げられます。
細かいところは置いておいて、まずは今からやりたいことの説明をしてみたいと思います。
先ほどまでの議論は、「推移確率行列を所与とした時、サイトに来てくれたユーザーはどのように動くか？」という記述が主眼に置かれていました。 一方、分析の目的によっては「推移確率行列が変化するとどのようにユーザーの動きが変わるか？」も知りたいはずです。例えば以下のようなシチュエーションを考えてみましょう：
- サイト内に「見て欲しいページ」（以下、目標ページ）がある
- 目標ページに辿り着きやすいように動線を改善したい
- どのリンクをクリックしやすくすれば、目標ページに辿り着きやすくなるだろう？
つまり、transitという遷移の仕組み（もっと言うと、推移確率行列であるtransit.W）が変化した時に、どのように結果の数値が変わるかを調べたい状況を想定します。
目標ページを決める
ここでは「採用情報ページ」を見て欲しいと仮定して、分析を進めてみます。
また仮定として、「同じユーザーが１回見てくれても、２回以上見てくれても、嬉しさは変わらない」とし、「採用情報ページを１回以上見てくれたユーザー」と、「採用情報ページを１度も見ずに離脱してしまったユーザー」を振り分けるようなシミュレーションをしてみたいと思います。
その目的を反映するために、推移確率行列をちょっとだけ書き換えてみます。
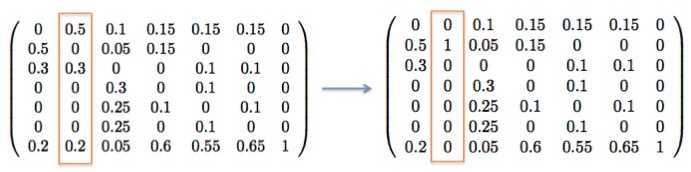
上記の行列のどこを書き換えたかというと、２列目の要素のみが変わっており、$(2, 2)$成分が$1$、その他の成分が$0$となっています。 これは目標ページである採用情報ページを、離脱状態と同様「一度入ったら出られない」状態に書き換えたということですが、これは「一度以上採用情報ページを見てくれたユーザー」と「そうでないユーザー」を区別するための方便です。
この場合の定常状態は、例えば以下のようになります。
採用情報ページに流入したユーザーは、その時点で「目標に到達した」ことが分かりますので、今回の目的の下では、目標到達以降の遷移のトラッキングは不要です。 採用情報ページに留まり続けるようにすることで、トラッキングの終了を表現しています。
また、結果的に何人が採用情報ページを見てくれるかというシミュレーション結果も、定常状態の分布をみれば一目瞭然です。（上記の例は、23人中12人が見てくれるという結果になっています。）
実際のシミュレーション結果を確認してみましょう。
markov_chain = MyMarkovChain(np.array([[0, 0, 0.1, 0.15, 0.15, 0.15, 0],
[0.5, 1, 0.05, 0.15, 0, 0, 0],
[0.3, 0, 0, 0, 0.1, 0.1, 0],
[0, 0, 0.3, 0, 0.1, 0, 0],
[0, 0, 0.25, 0.1, 0, 0.1, 0],
[0, 0, 0.25, 0, 0.1, 0, 0],
[0.2, 0, 0.05, 0.6, 0.55, 0.65, 1]], dtype=np.float32))
distribution = Variable(np.array([[10, 5, 1, 3, 2, 2, 0]], dtype=np.float32))
print markov_chain.transit_until_limit_distribution(distribution)
> ...
> Distribution after 19 th transition:
variable([[ 1.68337533e-06 1.23127584e+01 1.67016697e-06
1.39875044e-06 1.46680520e-06 1.21840844e-06
1.06872349e+01]])
あくまで近似計算であることと、丸め誤差から若干分かりにくいですが、 第２ページ（採用情報ページ）に約12.31人、離脱状態に約10.69人のユーザーがおり、他のページには殆どユーザーが残っていないことが分かります。 つまり、期待値において、初期分布 distributionと推移確率行列tpaの下で、採用情報ページを見てくれるユーザーは約12.31人であるという結果が導けます。
感度分析 - 推移確率行列の変化による影響
最後のトピックとして、推移確率行列markov_chain.transition.Wが変化したとき、結果がどのように変わるかを調べてみたいと思います。 例えば、TOPページからの離脱率を5%引き下げて、採用情報ページへの推移確率を5%高めることができたとしましょう。その場合、先ほどの計算結果における、目標ページ到達ユーザーは増加することが考えられます。 しかしその増加分が「どのくらいであるか」見積もるのは、あまり簡単ではなさそうですよね。
ところが、Chainerには強力な武器があります。計算過程の一部パラメータを変更した時、出力（今回の場合、定常分布）がどのように変動するかを調べることのできる計算手法である 誤差逆伝播法（Backpropagation） が関数として提供されているのです。
Tutorialでは最初のトピックとして出てくるくらいなので、ニューラルネットワークにおいては必須の計算なのですが、その原理の理解には微分の連鎖規則に関する知識が必要になりますので、今回は省略させて頂きます。
誤差逆伝播法の計算内容と、Chainerがこの計算をサポートできているカラクリについて、正確さを犠牲にしてざっくり説明するなら、以下のようになります：
- ChainerのVariable変数は値だけでなく、「現在の値が格納されるまでの計算過程」も保存してくれる
- なので、計算過程の一部パラメータが変化した時の影響を事後的に評価することが可能
- 評価の具体的なやり方は誤差逆伝播法に基づいており、パラメータの変動に対して出力がどのように変化するかを、出力結果から遡り影響を積算して見積もってくれる
一般に、「計算過程の一部パラメータが変わった時、出力がどのように変化するか？」を調べる分析を 感度分析 と言います。その際に重要なツールが 微分（ニューラルネットワークの文脈では 勾配計算 と呼ばれる）であり、誤差逆伝播法は長大な計算過程に対する勾配を計算するための技法です。 Chainerの誤差逆伝播法は感度分析を目的としたものではなく、確率的勾配降下法（SGD)等によるニューラルネットワークのパラメータ更新を主目的としていますが、いずれも本質的な操作は「微分（勾配計算）」です。この点も、マルコフ連鎖とニューラルネットワークのちょっとした共通点と言えそうです。
感度分析の実装
感度分析ができるよう、transit_until_limit_distributionを書き換えたものが下記コードです。
def transit_until_limit_distribution(self, dist_before_transit):
self.loop = self.loop + 1
dist_after_transit = self(dist_before_transit)
print "Distribution after", self.loop,"th transition:"
print dist_after_transit
dist_after_transit.grad = np.array([[0, 1, 0, 0, 0, 0, 0]], dtype=np.float32)
dist_after_transit.backward()
print "Sum of gradients up to", self.loop, "th transition:"
print self.transit.W.grad
if np.linalg.norm(dist_after_transit.data - dist_before_transit.data) < (10 ** -5):
self.loop = 0
return [dist_after_transit, self.transit.W.grad]
else:
return self.transit_until_limit_distribution(dist_after_transit)
追加した行について解説していきましょう。
重みの設定
dist_after_transit.grad = np.array([[0, 1, 0, 0, 0, 0, 0]], dtype=np.float32)
これは各ステップにおける遷移結果であるdist_after_transitについて、どの状態への到達を評価するか決めている行です。 今回は第２ページ（採用情報ページ）を目標ページに設定したので、第２成分のみを1とし、他のページを0としています。ここで複数の目標ページがあったり、それらの間に重みが存在する場合は、適宜設定を変更することができます。
注意 ニューラルネットワークの用途では、この数値は『初期誤差』と呼ばれます。例えば 岡谷(2015)において、p.49に$\delta^{(L)}_j$として定義されている数値に該当します。
誤差逆伝播法の実行
dist_after_transit.backward()
backwardはVariableオブジェクトに対して誤差逆伝播法を呼び出す関数です。dist_after_transit、すなわちそのループ時点で求まっている分布について、初期分布からの計算過程を全て追跡し、markov_chain.transition.W（推移確率行列）が変化した時の影響を微分計算により評価します。
結果の出力
print "Sum of gradients up to", self.loop, "th transition (gradient)"
print self.transit.W.grad
ループ毎に、その時点での影響の総和を出力します。
実行結果
markov_chain = MyMarkovChain(np.array([[0, 0, 0.1, 0.15, 0.15, 0.15, 0],
[0.5, 1, 0.05, 0.15, 0, 0, 0],
[0.3, 0, 0, 0, 0.1, 0.1, 0],
[0, 0, 0.3, 0, 0.1, 0, 0],
[0, 0, 0.25, 0.1, 0, 0.1, 0],
[0, 0, 0.25, 0, 0.1, 0, 0],
[0.2, 0, 0.05, 0.6, 0.55, 0.65, 1]], dtype=np.float32))
distribution = Variable(np.array([[10, 5, 1, 3, 2, 2, 0]], dtype=np.float32))
markov_chain.cleargrads()
limit_distribution, limit_effect = markov_chain.transit_until_limit_distribution(x)
> Sum of gradients up to 19 th transition (gradient)
> [[ 7.21651173 118.8604126 3.20709443 2.93544102 2.46638298 2.19952631 96.99636078]
> [ 12.53825283 222.91799927 5.57215118 5.10016489 4.2852087 3.82155728 182.76469421]
> [ 3.15799093 48.29377365 1.40343404 1.28455925 1.07929468 0.96251857 39.21710968]
> [ 3.15039349 51.00441742 1.40006709 1.28147614 1.07670712 0.96021003 41.57637024]
> [ 1.87185001 28.3139782 0.83186328 0.76140237 0.63973486 0.57051766 22.97503281]
> [ 1.5854516 23.93289566 0.70458531 0.64490521 0.54185313 0.48322648 19.41728973]
> [ 0. 0. 0. 0. 0. 0. 0. ]]
結果の解釈
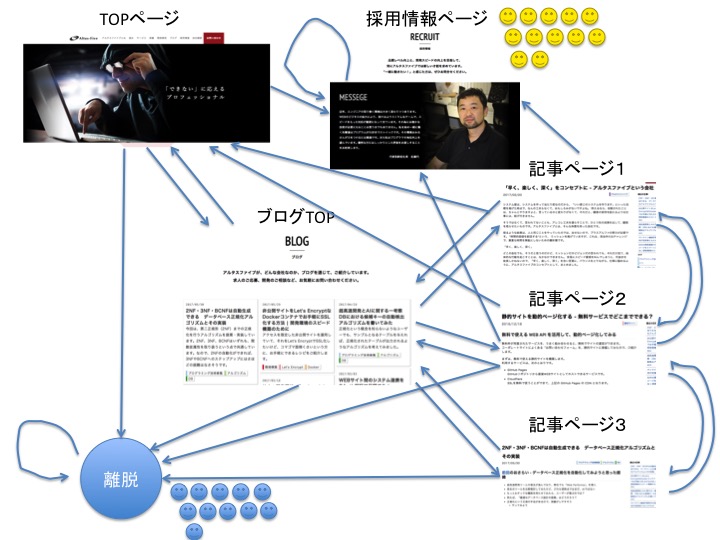
出力の$7 \times 7$行列は、推移確率行列(markov_chain.transition.W)と同じ形をしています。 これらの値は、対応する位置の推移確率が大きくなった時、目標ページ到達ユーザー数がどれくらい増えるかということを表す数値になっています。 数値をパーセンテージで解釈しやすくするため、値を100で割ってみます。
limit_distribution, limit_effect = markov_chain.transit_until_limit_distribution(x)
> Sum of gradients up to 19 th transition (devided by 100)
> [[ 0.07216512 1.18860412 0.03207095 0.02935441 0.02466383 0.02199526 0.96996361]
> [ 0.12538253 2.2291801 0.05572151 0.05100165 0.04285209 0.03821557 1.82764697]
> [ 0.03157991 0.48293772 0.01403434 0.01284559 0.01079295 0.00962519 0.39217108]
> [ 0.03150393 0.51004416 0.01400067 0.01281476 0.01076707 0.0096021 0.41576371]
> [ 0.0187185 0.2831398 0.00831863 0.00761402 0.00639735 0.00570518 0.22975034]
> [ 0.01585452 0.23932895 0.00704585 0.00644905 0.00541853 0.00483226 0.1941729 ]
> [ 0. 0. 0. 0. 0. 0. 0. ]]
上記の数値は、 「各推移確率を1%高めた時、目標ページ到達ユーザーが何人増えるか」 を示した数値になっています。 推移確率行列との対応付けを分かりやすくするため、上記の結果を行列形式で書いてみました。
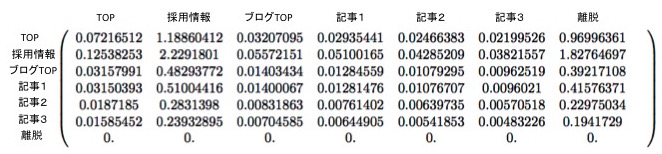
ただし、以下の遷移はネットワークの定義に反し、分析上意味がないので、考えないものとします。
- 離脱したユーザーが他のページに戻ってくる遷移
- 目標ページに到達したユーザー（トラッキングをやめたユーザー）が他のページに移動する遷移
- 同じページに止まるような遷移
これらの遷移に該当する箇所を隠して、結果を見やすくしてみましょう。
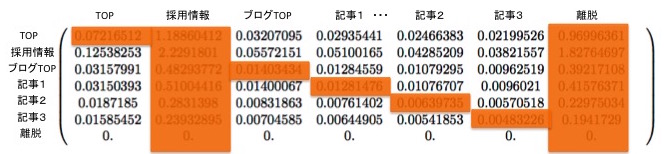
この行列を眺めてみると、以下のような傾向がつかめます。
- 第２ページ（採用情報ページ）への遷移を表す2行目の数値が特に大きい
- その次に、第１ページ（TOPページ）への遷移を表す1行目の数値が大きい
- 4, 5, 6行目（記事１, ２, ３への遷移）を比べると、記事１への遷移を表す４行目の数値が大きい
まず1.に関しては、第２ページは目標ページそのものですから、「他ページから第２ページへの遷移を増やせば、第２ページを見てくれるユーザーが増える」という当然の帰結となっています。 一方、2.や3.については興味深い結果です。第３ページ（ブログTOP）や第４〜６ページ（記事ページ）から、第１ページ（TOPページ）への遷移が増えると、無関係のはずの第２ページ（採用情報ページ）を見てくれるユーザーが増えることを示唆しています。 その理由は以下のように説明できます。第１ページ → 第２ページという動線はもともと太く、第１ページを見ているユーザーは50%もの確率で第２ページへ遷移してくれていました。つまり、第１ページは第２ページへの遷移をアシストしてくれる「つなぎ」のページとして優秀なのです。
この数値を解釈すると、 「第２ページ（採用情報ページ）に直接ユーザーを送り込むことがサイト設計上難しければ、まずは第１ページ（TOPページ）へ送りこむことを目標としても、第２ページ（採用情報ページ）を見てもらうという目標を達成することができる」 ということに気が付ける訳です。
3.についても同様です。第４ページ（記事１）は唯一、第２ページ（採用情報ページ）への遷移実績がある記事でした（推移確率行列を参照）。 このことから、 「もっと記事１を多くの人に読んでもらえれば、結果的に採用情報ページを見てくれる人が増える」 といったことも分かります。
まとめ
本記事は、２つの目的を同時に達成することを目的にまとめていきました。
- ニューラルネットワークの知識がなくても、Chainerのコードの書き方や挙動について何となく知ることが出来る
- ニューラルネットワークの近隣知識として、マルコフ連鎖について紹介する
両者のモデルには似ているところが多いので、面白い成果物が出来るのではないかと思いましたが、やはりニューラルネットワークに専心したライブラリ上で別の数理モデルを構築しましたので、少々実装について強引な部分もあったことを反省しています。
繰り返しになりますが、ニューラルネットワークを学ぶ目的であれば、マルコフ連鎖の学習はあくまで「寄り道」です。しかし、行列演算を直観的に解釈できる明快なモデルなので、行列演算に不慣れな方の取っ掛かりとしては適しているのではないかな、と思っています。
ニューラルネットワークの基礎理解には、本記事で解説した内容（行列演算）に加えて、以下の知識が必須になります。
- 活性化関数
- 誤差関数
- 誤差関数最小化アルゴリズム（確率的勾配降下法など）
- 勾配計算
- 誤差逆伝播法
上記は、Chainer TutorialのOptimizer以降の項を理解しながら読む時点で必要になります。やはり敷居の高さは感じざるを得ませんが、下記文献の４章までを読んでいけばカバー出来ます。興味のある方は、挑戦してみてください。
ソースコード
本記事の最終的な成果（感度分析）を実行出来るソースコードを公開します。 実行にはChainerのインストールが必要ですので、ご注意ください。
#!/usr/bin/env python
# -*- coding: utf-8 -*-
class MyMarkovChain(Chain):
def __init__(self, tpm):
super(MyMarkovChain, self).__init__()
if tpm.shape[0] == tpm.shape[1]:
dim = tpm.shape[0]
with self.init_scope():
self.transit = L.Linear(dim, dim)
self.transit.W.data = tpm
self.loop = 0
def __call__(self, dist):
return self.transit(dist)
def transit_designated_times(self, dist, times):
temp = dist
for num in range(times):
temp = self(temp)
return temp
def transit_until_limit_distribution(self, dist_before_transit):
self.loop = self.loop + 1
dist_after_transit = self(dist_before_transit)
print "Distribution after", self.loop,"th transition:"
print dist_after_transit
if np.linalg.norm(dist_after_transit.data - dist_before_transit.data) < (10 ** -5):
dist_after_transit.grad = np.array([[0, 1, 0, 0, 0, 0, 0]], dtype=np.float32)
dist_after_transit.backward()
print "Sum of gradients up to", self.loop, "th transition (devided by 100)"
print self.transit.W.grad / 100
self.loop = 0
return [dist_after_transit, self.transit.W.grad]
else:
return self.transit_until_limit_distribution(dist_after_transit)
markov_chain = MyMarkovChain(np.array([[0, 0, 0.1, 0.15, 0.15, 0.15, 0],
[0.5, 1, 0.05, 0.15, 0, 0, 0],
[0.3, 0, 0, 0, 0.1, 0.1, 0],
[0, 0, 0.3, 0, 0.1, 0, 0],
[0, 0, 0.25, 0.1, 0, 0.1, 0],
[0, 0, 0.25, 0, 0.1, 0, 0],
[0.2, 0, 0.05, 0.6, 0.55, 0.65, 1]], dtype=np.float32))
distribution = Variable(np.array([[10, 5, 1, 3, 2, 2, 0]], dtype=np.float32))
print markov_chain.transit_until_limit_distribution(distribution)
markov_chain.cleargrads()
limit_distribution, limit_effect = markov_chain.transit_until_limit_distribution(x)
関連記事
- 2018/07/18 全文検索を自社サイト・社内サーバーに構築したいクライアントのための留意点 システム開発における「全文検索」の実装方式・コスト・性能に関して、クライアント企業の方にも腹落ち頂けるようまとめました。grep型と索引型の違いに関する平易な解説を記載しているので、これらをクライアントに解説されたい開発者にもオススメです。
- 2018/02/01 利益管理のためのデータ可視化 技術者にできる事は何か？ データ可視化は科学技術分野において発祥した技術であり、与えられたデータから自動的に「見やすい図示」を出力するアルゴリズムを指します。データを見やすくし、ビジネスの意思決定に活用するという観点から手法を紹介し、R言語によるデモを行います。
- 2017/12/28 機械学習・統計学・最適化の違いについてまとめてみた 「機械学習」という手法は、システム開発の現場で用いられる事例が急増しています。一方、「統計学」という分野も機械学習と同様にデータを扱い、やはり多数の事例があります。本記事は「機械学習と統計学の違い」について整理することを試みます。
- 2017/12/04 システムによる最適化を通じて、開発者がめざすもの 〜エレベーターの制御システムを例に〜 システム開発においてお客様の要望に応えようとするとき、いろいろなところで「システムによる最適化」を含む開発アイデアを発想します。この記事では、最適化を成り立たせる「目的関数」と「制約式」という思考法を紹介します。
- 2017/05/30 2NF・3NF・BCNFは自動生成できる データベース正規化アルゴリズムとその実装 今回は、第二正規形（2NF）までの正規化を行うアルゴリズムを提案・実装しています。2NF、3NF、BCNFはいずれも、関数従属性を取り扱うという点で共通しています。なので、2NFの自動化ができれば、3NFやBCNFへのステップアップにはさほどの困難はなさそうです。